LOG 関数
Microsoft Excel の LOG 関数 の使い方を説明します。
対数とは何か、その基本的な考え方を説明します
LOG 関数
- LOG
- [読み]:ログ
- [英語]:LOGarithm
- [書式]:=LOG(<数値>,<底>)
- この関数は指定した<底>に対する<数値>の 対数 を返します
- 対数とは<底>を何回掛けたらその<数値>になるかを表しています、
詳しくはこの少し下に説明 → [対数とは]
LOG 関数 の例
- LOG 2 8 を求める例:
セルA2に 8 が入力され、セルB2に 2 が入力されている時、セルC2 に =LOG(A2,B2) と入力すると、LOG 2 8 が計算され、3 が返されます 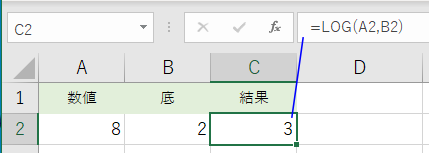
- LOG 3 81 を求める例:
セルA2に 81 が入力され、セルB2に 3 が入力されている時、セルC2 に =LOG(A2,B2) と入力すると、LOG 3 81 が計算され、4 が返されます 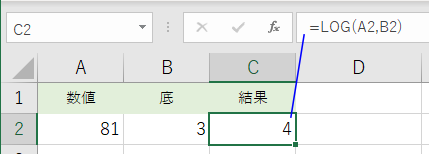
- [常用対数] LOG 10 100 を求める例:
セルA2に 100 が入力され、セルB2に 10 が入力されている時、セルC2 に =LOG(A2,B2) と入力すると、LOG 10 100 が計算され、2 が返されます 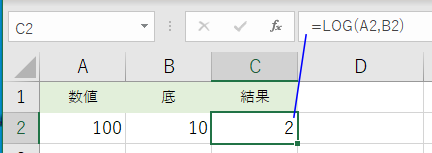
- [常用対数] LOG 100 を求める例:
セルA2に 100 が入力されている時、セルB2 に =LOG(A2) と入力すると、
LOG 100 が計算され、2 が返されます。
底は省略することができ、省略すると 底 = 10 で計算されます。 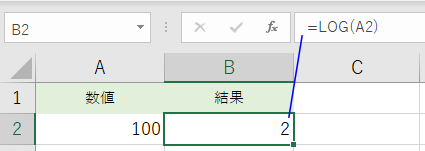
- LOG 3 4 を求める例:
セルA2に 4 が入力され、セルB2に 3 が入力されている時、セルC2 に =LOG(A2,B2) と入力すると、LOG 3 4 が計算され、1.26186 が返されます 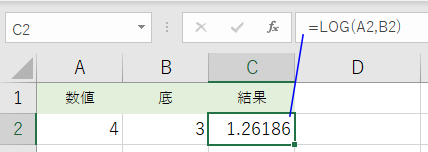
対数とは
対数とは<底>を何回掛けたらその<数値>になるかを表しています
- 8 は 2 x 2 x 2 のように2を3回掛けると求まるので
LOG 2 8 = 3 と書きます
- 81 は 3 x 3 x 3 x 3 のように3を4回掛けると求まるので
LOG 3 81 = 4 と書きます
- 100 は 10 x 10 のように10を2回掛けると求まるので
LOG 10 100 = 2 と書きます
- このようにLOG の右下に小さく書いたものを 底 と呼び、
LOG の右側に書いたものを 真数 と呼びます
対数の基本公式
- LOG a a = 1
- LOG a 1 = 0
- LOG a ( x y ) = LOG a x + LOG a y
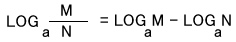
- LOG a x m = m LOG a x
常用対数
- 常用対数:Common logarithm
- <底>が10の対数は、常用対数と呼ばれます
- 常用対数の場合、<底>を略すことがあります
- LOG 10 100 = LOG 100 = 2
- 常用対数の場合
86 → =LOG(86,10) → 1.934498
86 → =LOG(86) → 1.934498
86 → =LOG10(86) → 1.934498
自然対数
- 自然対数:Natural logarithm
- <底>が 定数 e (2.7182818) の対数は、自然対数と呼ばれます
- 自然対数の場合
86 → =LOG(86,2.7182818) → 4.4543473
86 → =LN(86) → 4.4543473
86 → =LOG(86,EXP(1)) → 4.4543473
1分間で2つに増える細菌が1億匹になるのは何分後?
- LOG 2 100000000
- = LOG 2 10 8 (↑の基本公式5. から)
- = 8 LOG 2 10
- = 8 * 3.321928
- = 26.57542
- この例では、1分間で2つに増える細菌が約27分後に1億個になることを表しています
LOGのおかげで、大きな桁の数を扱うことができます
- N = 4 50 を求める例
- LOG 10 N = 50 * LOG 10 4
- = 50 * 0.60205999
- = 30.1029996
- 桁数は 30 となり、小数点以下 は10 0.1029996 なので 1.2673 になり
- 最終的に N は 1.2673 x 10 30 になります
- このように 対数 LOG というものがあるので、大きな桁の数を扱うことができるのです
LOGは大きな桁の数値の比較を扱いやすくする
- 両対数グラフを描きたい (tp0025)
- この例でわかるようにLOG[対数]は 1 10 100 1000 10000 と 過激に増えてゆくようなデータを比較するためのものです
関連サイト
- 受験のミカタ: 対数関数とは?logの基礎から公式まで
- おしえて!goo: LOGについて
- Yahoo!知恵袋: 自然対数と常用対数の使い分けを簡単に...
- support.microsoft.com: LOG 関数
- WikiPedia:
対数、 常用対数、 自然対数
キーワード
- LOG
- ln
- logarithm
- Common logarithm
- Natural logarithm
- 対数
- 底
- 真数
- 常用対数
- 自然対数