STDEV 関数
Microsoft Excel の関数 STDEV STDEVP の使い方を説明します、
この関数は 母集団の標準偏差 を返します
STDEV 関数
- STDEV
- [語源]:STandard DEViation
- [読み]:スタンダード・ディービエーション
- [書式]:=STDEV( [数値1] , [数値2] ... )
-
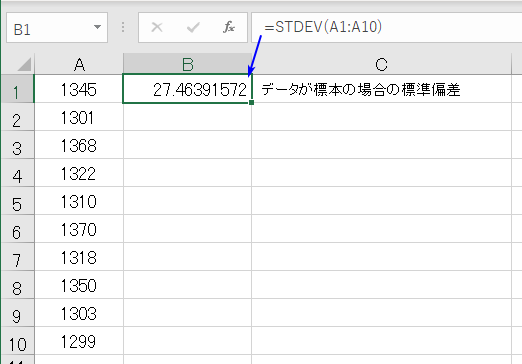
この関数は データを母集団の標本と見なして、母集団の標準偏差 を返します
- 標準偏差 は平均値からの散らばり度合いを表します
- =STDEV(A1:A10) では データ範囲 A1からA10 を 母集団の標本と見なして 母集団の標準偏差 27.46391572 を返します
-
STDEVP 関数
- STDEVP
- [語源]:STandard DEViation Population
- [読み]:スタンダード・ディービエーション・ピー
- [書式]:=STDEVP([数値1],[数値2]...)
-
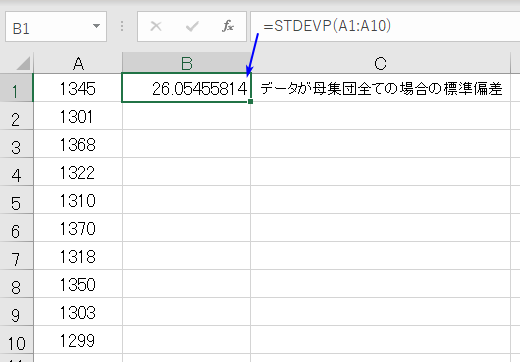
この関数は データを母集団全てと見なして、母集団の標準偏差 を返します
- 標準偏差 は平均値からの散らばり度合いを表します
- =STDEVP(A1:A10) では データ範囲 A1からA10 を 母集団全てと見なして 母集団の標準偏差 26.05455814 を返します
-
STDEV と STDEVP の使い分け
-
STDEV
- 標本標準偏差
- データが母集団の標本の場合に使います
- こちらが一般的に標準偏差と呼ばれます
-
STDEVP
- 母標準偏差
- データが母集団全ての場合に使います
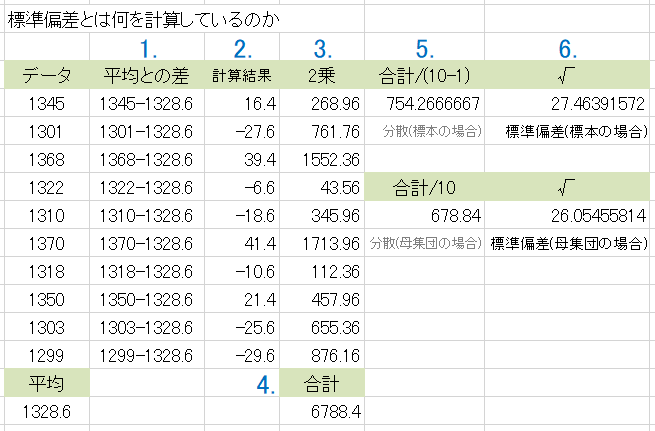
標準偏差とは何を計算しているのか
- 標準偏差は一体何を計算しているのか
-
- 1. 2. データと平均との差を求め
- 3. 結果を2乗して
- 4. その総和を求めて
- 5. データ数で割ります、標本では 10-1=9 で割り、母集団全体では 10 で割ります
- 6. その平方根
-
標準偏差って何
- 標準偏差は 平均値からのデータの散らばり度合い を表します
- この標準偏差を一般的に σ (シグマ) で表します
- 標準偏差が小さければ 散らばり具合が小さい といえます
-
正規分布に従うデータの場合データが存在する確率は下のようになります
- 1σ :平均 + σ と 平均 - σ の間に:68.3%
- 2σ :平均 + 2σ と 平均 - 2σ の間に:95.4%
- 3σ :平均 + 3σ と 平均 - 3σ の間に:99.7%
- 上の関数で求めた例では 標準偏差 = 27.5 なので 原理的には 1328.6 - 27.5 と 1328.6 + 27.5 の間に全体の 68.3% のデータが存在するということです
-
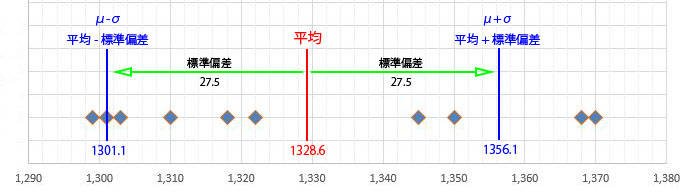
上の関数で求めた例を実際にプロットしてみると
1328.6 - 27.5 = 1301.1 と 1328.6 + 27.5 = 1356.1 と の間に全体の
(6.5 / 10) = 65% のデータが存在しています
- (確かに68.3%に近い値になっています)
-
3σ (3シグマ)
3σ:μ - 3σ と μ + 3σ の間にほとんどのデータが入ると言うことです
- 上の例では σ = 27.5 なので 3σ は σ の 3倍 ですから 3 * 27.5 = 82.5
- μ - 3σ = 1328.6 - 82.5 = 1246.1
- μ + 3σ = 1328.6 + 82.5 = 1411.1
- 正規分布に従うデータの場合 1246.1 から 1411.1 の間に 99.7% のデータが存在する事になります
STDEV.S と STDEV.P について
Excel2010 以降 STDEV が STDEV.S にSTDEVP が STDEV.P に更新されました、以前のバージョンで動かす可能性がなければ移行するのが良いでしょう。- STDEV → STDEV.S
- STDEVP → STDEV.P
関連ページ
- [[20150504193226]] 『標準偏差値』(迷人)
- [[20041116130142]] 『偏差値の求め方:標準偏差が分かりません』(頭痛)
- [[20040316211408]] 『標準偏差は2つの値から計算できますか?』(サイ)
- 偏差値 (tp0051)
- VAR関数 母集団の分散を返す
関連サイト
キーワード
- 標準偏差
- 標本標準偏差
- シグマ
- σ
- 1σ
- 2σ
- 3σ
- 計算
- 標本
- 母集団
- STDEV
- STDEVP
- standard deviation
- standard deviation population
- 関数